By Kelvin Yuk and Jackie Xue
Originally published Mar 12, 2003
Introduction
In our project, we explore two different circuit design optimization techniques. We first implement the steepest descent algorithm to exemplify some of the basic concepts in circuit network optimization. The resistors of a simple DC network are optimized to meet a desired output voltage. An optimization is also performed on a simple RC low-pass filter circuit to show how steepest descent can be used to optimize AC. Since the steepest descent method can have difficulty in converging, we next discuss the conjugate-gradient method and implement the algorithm to optimize a single transistor amplifier.
Steepest Descent
In a circuit design program, the performance function is a measure of the error between the desired network response and the actual network response. The objective of this computer-aided design (CAD) program is to adjust the elements of the network to minimize the value of the performance function.
One method to minimize the performance function is to use steepest descent, which we have gone over in class. The steepest descent is in good use only when the equierror contours are perfect circles as shown in Figure 1. The figure shows that only one iteration is required to reach the minimum because the negative gradient direction points directly at the minimum. However, if the contours are elongated as shown in Figure 2, the gradient direction can almost parallel the path that leads directly to the minimum and a very large number of iterations are required to reach the minimum.
The steepest method uses one-dimensional search to find the minimum of ε(P) along a give direction Sj. The search wishes to find the value of αj for which ε(Pj + αS) is minimized. Note that ε(Pj + αS) is a function of α:
![]() And we want to seek α such that
And we want to seek α such that
The first step in the search is to bound the minimum (αl, αu), called extrapolation. Then the constraint is
![]() for all values of α such that αl ≤ α ≤ αu. The search starts by initially choosing a small step size, say α0, f(α0) then doubling the step size and evaluating f(2α0), then doubling the step size again and evaluating f(4α0), etc., until there is an increase in error, that is, f(2jα0 < f(2(j+1)α0) [1].
for all values of α such that αl ≤ α ≤ αu. The search starts by initially choosing a small step size, say α0, f(α0) then doubling the step size and evaluating f(2α0), then doubling the step size again and evaluating f(4α0), etc., until there is an increase in error, that is, f(2jα0 < f(2(j+1)α0) [1].
The search starts to observe the values f(αl), f(αu), df/dα|αl, and df/dα|αu to define a cubic curve once αl and αu have been found. The value of α minimizes the cubic curve and this value of α is given by
 Matlab Implementation of Steepest Descent
Matlab Implementation of Steepest Descent
The Steepest Descent method was implemented in Matlab. The function that runs the steepest descent algorithm is shown in Figure 3. The user inputs an initial guess of the parameter set P0, a set of frequencies w, the corresponding target output voltages Vout_bar and the output node to optimize Vo_node.
function [P,eps] = opt_steep(P0,w,Vout_bar,Vo_node)
%the vector P0 must be a column vector
P=P0
eps = get_error(P,w,Vout_bar,Vo_node) %initialize eps
%iterative loop here
for iter=1:10
%compute the gradient
G=grad(P,w,Vout_bar,Vo_node)
%compute magnitude of the gradient
G_mag = 0;
for i=1:length(G)
G_mag = G_mag + G(i)^2;
end
G_mag = sqrt(G_mag);
%find direction vector S
S = -G’/G_mag;
%start guessing with alpha and compute the p’s and eps
alpha0 = 1e-4;
alpha = alpha0;
while(1)
%solve for the new P values
Pnew = P + alpha.*S;
for k=1:length(Pnew)
if (Pnew(k)<0)
zero=1;
else
zero=0;
end
end
if (zero==1)
break;
end
epsnew = get_error(Pnew,w,Vout_bar,Vo_node);
if(eps < epsnew)
disp(‘eps is < eps new’)
Pnew=P+(alpha-alpha0).*S
break;
end
eps = epsnew;
alpha=alpha+alpha0;
end
P=Pnew;
end
Figure 3. opt_steep.m
The program first calculates the initial error corresponding to the initial guess of the parameters. The error is calculated in the function get_error which is shown in Figure 4. In the get_error.m function, the node voltages of the circuit are solved with the given parameter set. The error is then calculated using from
![]() Note that the error is takes into account all frequencies by summing the squared difference of the solved and target output voltages. The node voltages of the network is solved using the function solve_net.m shown in Figure 5. The inputs to solve_net are the parameter set and a single frequency value. The function contains the current source, solves the nodal admittance matrix Y using the parameter set and computes the nodal voltages at the specified frequency.
Note that the error is takes into account all frequencies by summing the squared difference of the solved and target output voltages. The node voltages of the network is solved using the function solve_net.m shown in Figure 5. The inputs to solve_net are the parameter set and a single frequency value. The function contains the current source, solves the nodal admittance matrix Y using the parameter set and computes the nodal voltages at the specified frequency.
function eps=get_error(P,w,Vout_bar,Vo_node)
% Initialize Error
eps=0;
% Calculate Performance function and gradient
for idx=1:length(w)
% Solve original network
[V,Y,I]=solve_net(P,w(idx));
eps = eps + (abs(V(Vo_node))-abs(Vout_bar(idx)))^2;
end
eps = 0.5*eps;
Figure 4. get_error.m
function [V,Y,I]=solve_net(P,w)
% Initialize element values
R1=P(1);
R2=P(2);
C1=P(3);
Y = [(1/R1+1/R2) (-1/R2); (-1/R2) (1/R2+j*w*C1)];
I = [1;0];
V=inv(Y)*I;
Figure 5. solve_net.m
The iteration loop begins and the gradient is calculated using the function grad.m which will be discussed later. The resulting gradient G is used to calculate the directional vector S which is used for incrementing the parameter set. The directional vector S
![]() is then used as the direction for which the parameter set is incremented. An alpha is incremented to compute the new parameter set, and the error is computed every time until the a minimum error is reached.
is then used as the direction for which the parameter set is incremented. An alpha is incremented to compute the new parameter set, and the error is computed every time until the a minimum error is reached.
function G=grad(P,w,Vout_bar,Vo_node)
% Initialize Gradient
G=zeros(1,length(P));
% Calculate Performance function and gradient
for idx=1:length(w)
% Solve original network
[V,Y,I] = solve_net(P,w(idx));
R1 = P(1);
R2 = P(2);
C1 = P(3);
% Calculate branch voltages and currents needed for gradient computation
I_R1 = V(1)/R1;
I_R2 = (V(1)-V(2))/R2;
V_C1 = V(2);
T=(abs(V(Vo_node))-abs(Vout_bar(idx)))*conj(V(Vo_node))/abs(V(Vo_node));
% Set up Adjoint Network Excitation
PHI=[0;1];
% Compute Adjoint Network Voltages and Currents
Y_hat = Y’;
PSI = inv(Y_hat)*PHI;
PHI_R1 = PSI(1)/R1;
PHI_R2 = (PSI(1)-PSI(2))/R2;
PSI_C1 = PSI(2);
%Summation of gradients for all freqs
G(1)=G(1)-P(1)*real(T*PHI_R1*I_R1);
G(2)=G(2)-P(2)*real(T*PHI_R2*I_R2);
G(3)=G(3)+P(3)*real(T*j*(w(idx))*V_C1*PSI_C1);
end
Figure 6. grad.m
The gradient function is shown in Figure 6. The inputs are the parameter set P, frequency points w, desired output voltages Vout_bar and output node Vo_node. For every frequency point, the node voltages of the circuit are found. From them the needed branch currents are found depending on the component type. Then, the f0 as discussed in lecture is found. This variable is needed to compute the gradients. Next, the adjoint network is set up and analyzed. The adjoint network’s nodal admittance matrix is simply the transpose of the original network’s nodal admittance matrix. The currents and node voltages, F and Y, respectively, are solved as well as the needed branch currents. Finally, the gradients are summed for each component. Since the components can differ, the component sensitivities used to compute the gradients can differ. In our example code above, the resistors and capacitors are used. The sensitivities of the resistor and capacitor are
![]() The sensitivities of other components are not included here but can be referred back to lecture. We use only resistors and capacitors in the steepest descent application to maintain simplicity. Another thing to note here is that we multiply the component value to the sensitivity in the gradient computation because this implements logarithmic scaling where
The sensitivities of other components are not included here but can be referred back to lecture. We use only resistors and capacitors in the steepest descent application to maintain simplicity. Another thing to note here is that we multiply the component value to the sensitivity in the gradient computation because this implements logarithmic scaling where
![]() Logarithmic scaling is useful for when the components are not within the same magnitude range.
Logarithmic scaling is useful for when the components are not within the same magnitude range.
DC Example
The steepest descent algorithm was performed on a DC circuit as shown in Figure 7. The DC circuit is a simple resistive network with three resistors and one current source. The circuit was first simulated in HSPICE with the resistor values shown in Figure 7 to find the output voltage. The resulting output voltage is 0.5V.
The resistor values R1=2ohm, R2=16ohm and R3=6ohm serve as a basis for which we perform dc optimization. In our optimization example, we begin with a set of parameters that do not give the correct output to serve as our initial guess. The parameters selected are R1=5ohm, R2=1ohm and R3=4ohm. The resulting output voltage as simulated in HSPICE is 2V. Then, the steepest descent optimization routine is called and the gradients are computed. The gradients are computed from the network and the adjoint network as shown in Figure 8. Once the gradients are computed, the descent direction is computed and the parameters are incremented until a convergent set is found.
The resulting parameter set is R1=2.5ohm, R2=1.5ohm R3=1ohm. Although this is not the same set as we began with, it produce the optimized output voltage when simulated in HSPICE. A summary of the parameters and results are shown in Table 1 below.
AC Example
An AC example of the steepest descent algorithm was also performed. Consider the simple RC low pass filter circuit shown in Figure 9. An ac analysis of the circuit with the component values shown in the figure was performed to establish a target output voltage characteristic. The frequency of the input signal was varied from 1rad/s to 10e3 rad/s. The ac analysis was performed using the solve_net function of the optimization program over the range of input frequencies.
An intentionally incorrect initial guess of the parameters was made and used as a starting point for the optimization. The parameters in the initial guess are R1=1ohm R2=2ohm and C1=100e-4F. We ran the optimization routine with this set of parameters and observed if it converged to a correct solution. The resulting optimized parameter values were R1=1.0062, R2=1.9935 and C1=2e-4F. A summary of the parameters and error values are shown in Table 2.
The frequency responses of all three parameter sets are shown in Figure 10. We can see that the initial guess gave a high error with a response that is far from the desired response. However, the optimized solution is fairly close to the desired response. Although the optimized parameters are not the same as the ones we began with to produce the desired response characteristic, the results are still fairly close.
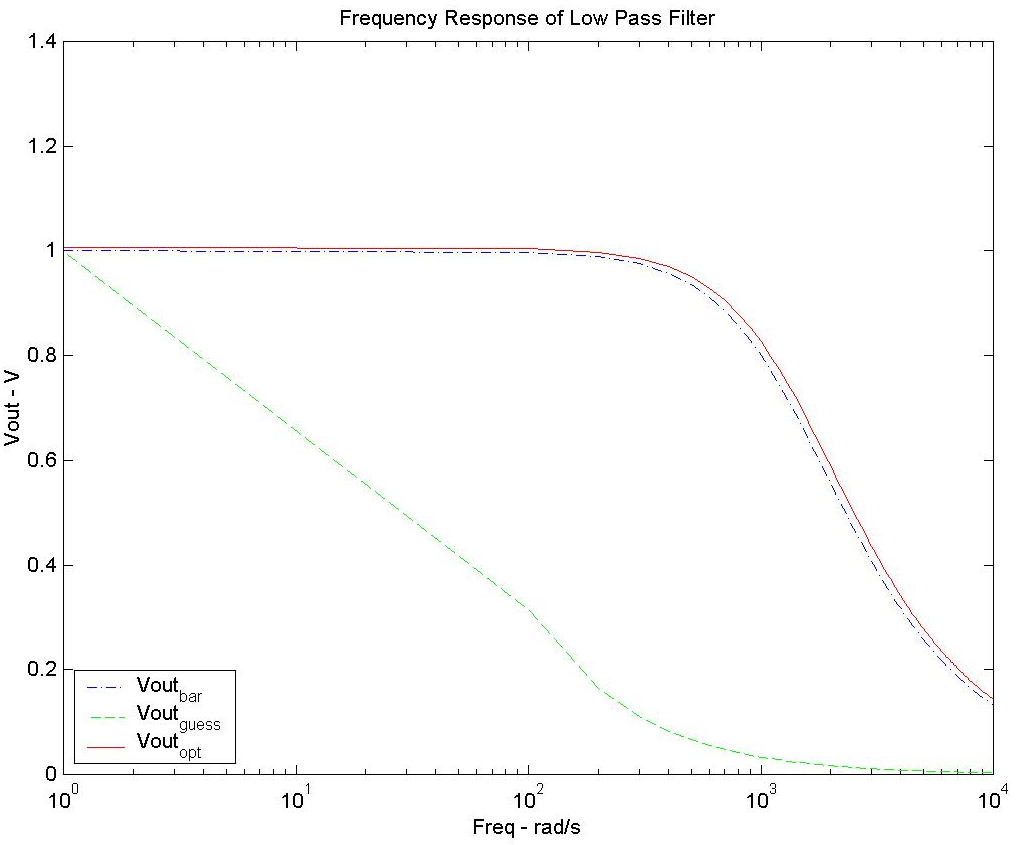
Figure 10. Frequency response of the desired, guessed, and optimized parameter sets for the AC analysis example
Conjugate Gradients Method
Since the steepest descent is not good for finding the minimization of an error function if the error contours are elongated, we can avoid this problem using the conjugate gradients method. Since this method is more powerful than steepest descent, we briefly explain the algorithm as well as implement and perform an example to demonstrate its capability. We first discuss the basic algorithm to establish an understanding of the conjugate gradient algorithm.
The algorithm shown in Figure 11 summarizes the conjugate gradient method. In the step (1) of the algorithm, the parameter set is first chosen as P0. In step (2), Ñe0, gradient of the set P0, is calculated and the directional vector S0 is initially set to the negative gradient. In step (3), the error function e(P) is calculated and the parameter set is incremented in the direction Si until the minimum error is found. The parameter set at that minimum error is saved. In step (4), a new gradient for the minimum parameter set found in step (3) is calculated. In step (5), a beta scaling factor is calculated from the square of the new gradient from step (4) divided by the square of the gradient from step(2). Finally, a new directional vector is calculated from the negative of the new gradient and the old direction scaled by beta. The iteration counter is incremented and steps (3) through (6) is repeated until the solution set converges. We observe that the directional vector is computed not only from the gradient itself, but also from previous directional information.
The algorithm can be used for any general function. Since we apply it on the error function, the choice of P0, the linear search to locate each Pi+1, the overall rate of convergence and the final convergence criterion must be taken to account. For more information on the algorithm, please reference [2] and [3].
Conjugate Gradient Implementation
A subroutine CNJGRD is the implementation of the conjugate gradient minimization algorithm in Fortran IV programming language [1]. We have modified the subroutine from Fortran IV into a function in MATLAB for our own use to solve DC and AC optimization of our examples. The code for the conjugate gradient algorithm and single transistor example is included at the end of this report. It is very complicated and included only for completeness. The syntax for calling function CNJGRD is
[P, F, G, S, IER] = CNJGRD (N, P, EST, EPS, LIMIT, PR, nf, freq, desout)where
N – the number of adjustable parameters
P – an array of parameters values
F – a variable that contains the final value of the performance function
G – an array in the calling program that stores the gradient of the performance function
S – an array that stores the new updated parameters and old parameters values
EST – an estimate of the minimum value of F
EPS – an estimate of how many significant digits of accuracy are required for convergence, a good value is 10-9
LIMIT – the maximum number of iterations
IER – a return value between 1 and 3 from the function to indicate the following condition:
IER = 1, convergence is occurred
IER = 2, maximum number of iteration is exceeded
IER = 3, error in gradient calculation
PR – a variable is set to true will cause the function to display F each time the performance function is evaluated
nf – the number of frequency point to evaluate in the circuit
freq – an array of frequency value to evaluate
desout – an array of desire output corresponds to the freq array
Inside the function CNJGRD, it calls functions SOLVE_NET and PRMCHG. Function SOLVE_NET returns the values of the performance function and its gradient for each parameter by analyzing the original and adjoint network. Further discussion on the SOLVE_NET function will be later. The syntax for calling function SOLVE_NET is
[F, G] = SOLVE_NET (N, P, icount, nf, freq, desout)
where icount is the variable to indicate the number of iterations and also can be use to tell the function to display and plot of the final values of output. Function PRMCHG is to use to change the parameter array P along the direction S using a step size of AMBDA. The syntax for calling it is
[P] = PRMCHG (P, AMBDA, S, N)
Conjugate Gradients Example
The conjugate gradients method was applied on the single transistor amplifier shown in Figure 12. The amplifier is a common emitter amplifier. The amplifier is optimized using the hybrid-pi model as shown in Figure 13. The initial guessed parameters and the optimized parameters are shown in Table 3. It shows that the conjugate gradients method was able to reduce the initial error of 7051.717096417715 down to 32.2009 after three iterations.
The frequency response of the amplifier is shown in Figure 14. It shows the desired response, the initial response and the final optimized response. We can see that at lo frequencies, the initial guess gave an extremely poor gain of around 13dB as opposed to the desired 40dB. Although the target response is ideal, we see that the optimized parameters brings the gain to almost as high as desired. The gain at low frequencies is 40dB and the cutoff frequency is around 500kHz. The desired curve has a very sharp descent due to the lack of data points and the fact that it is not based on any existing set of parameters and so the optimized curve comes close to realizing it.
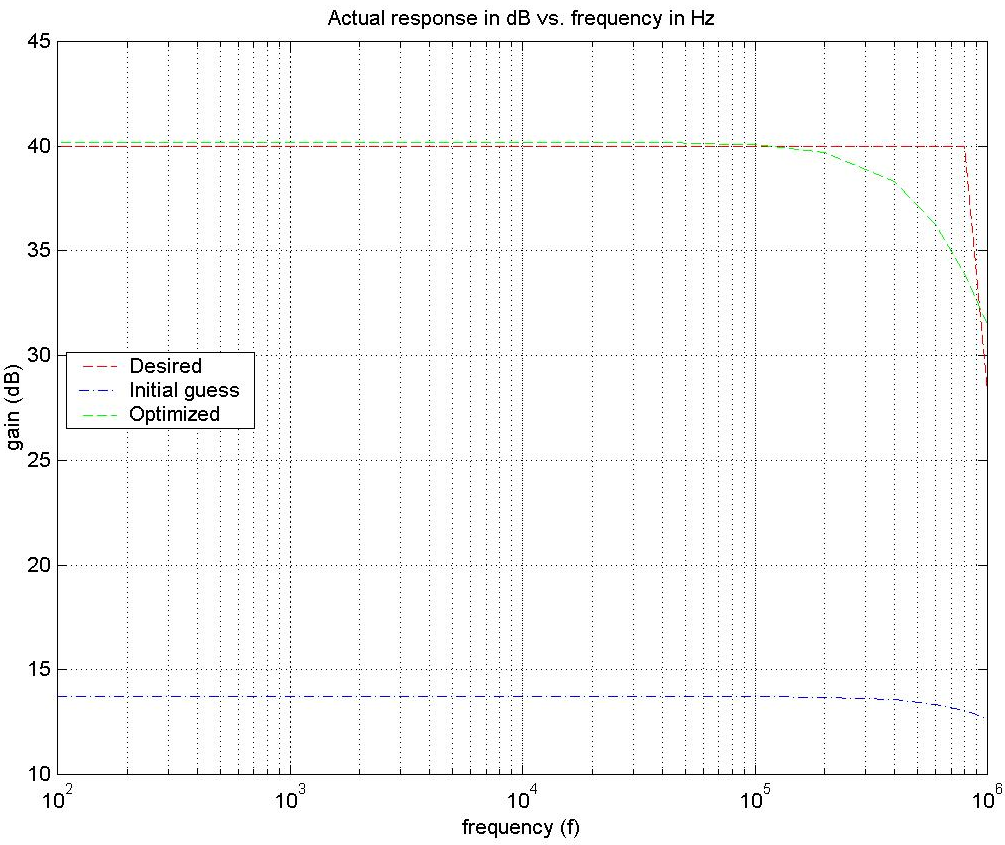
Figure 14. Frequency response for the Transistor optimization example demonstrating the conjugate gradient method.
Conclusion
We have explored two different methods of optimization and shown different examples of each method. It was very difficult to implement the algorithm into a working example and the results that were obtained are not perfect. The convergence of the parameters to a minimum error is a difficult task and the resulting parameter set and convergence seems to be largely dependent on how close the initial guess it. The implementation presented here are far from a well-developed general purpose program but it demonstrates the capabilities of these optimization algorithms into a practical circuit application.
References
[1] Stephen W. Director, “CIRCUIT THEORY A Computational Approach,” John Wiley & Sons, Inc, 1975.
[2] R. Fletcher and C. M. Reeves, “Function minimization by conjugate gradients”, Computer Journal, Vol. 7, pp. 149-154, 1964.
[3] R. Fletcher and M. J. D. Powell, “A rapidly convergent descent method for minimization”, Computer Journal, Vol. 6, pp. 163-168, 1963

















